
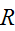 ,
consisting of all pairs
,
consisting of all pairs

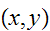 where
where

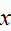 and
and

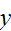 are bit strings of length three or more that agree except perhaps in their
first three bits, is an equivalence relation on the set of all bit strings.
are bit strings of length three or more that agree except perhaps in their
first three bits, is an equivalence relation on the set of all bit strings.
Show that the relation

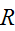 ,
consisting of all pairs
,
consisting of all pairs

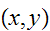 where
where

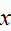 and
and

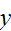 are bit strings of length three or more that agree except perhaps in their
first three bits, is an equivalence relation on the set of all bit strings.
are bit strings of length three or more that agree except perhaps in their
first three bits, is an equivalence relation on the set of all bit strings.
Solution:
To show this, we need to show that the relation

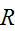 is reflexive, symmetric, and transitive.
is reflexive, symmetric, and transitive.
Let

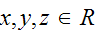 be bit strings that differ at most in their first three bits.
be bit strings that differ at most in their first three bits.
Reflexive: It is reflexive because after the first 3 bits,

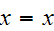
Symmetric: It is symmetric because after the first 3 bits,

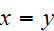 and
and

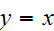
Transitive: It is transitive because

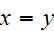 and
and

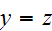 ,
therefore
,
therefore

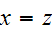
Since

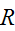 is reflexive, symmetric, and transitive,
is reflexive, symmetric, and transitive,

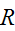 is an equivalence relation.
is an equivalence relation.