
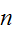 vertices and
vertices and

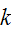 connected components has at most
connected components has at most

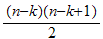 edges.
edges.
Use Excercise 35 to show that a simple graph with

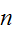 vertices and
vertices and

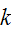 connected components has at most
connected components has at most

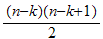 edges.
edges.
Solution:
Excercise 35 proved that a simple connected graph has

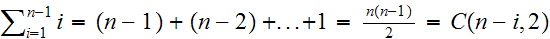
edges.
A simple graph with

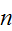 vertices and
vertices and

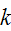 connected components has at least
connected components has at least

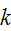 vertices, ie
vertices, ie

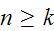 .
.
The amount of edges in such a
graph are maximized when a single component has the maximum amount of vertices
and still satisfies

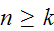 .
.
In this case, every component will have only one vertex, except one, which has all of the other vertices.
All components except one will have no edges.
The other component will have

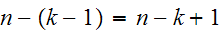 vertices.
vertices.
If we put this into the formula
from #35, we have

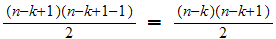 edges.
edges.